Monument Draw

AcapulcoitePrimitive achondrite that belongs to a small group named after the Acapulco meteorite that was observed to fall in Mexico in 1976. Acapulcoites are made mostly of fine-grained olivine (Fo3-14), orthopyroxene(En86-97), Ca-rich pyroxene (En51Wo44), plagioclase (An12-31), Ni-Fe metal, and troilite. They are transitional between primordial chondritic matter and more differentiated, primitive subgroup
Acapulcoite–LodraniteRare type of primitive achondrite named after the Lodran meteorite that fell in Pakistan in 1868. Initially, lodranites were grouped with the stony-iron meteorites because they contain silicates (olivine, orthopyroxene, and minor plagioclase) and Fe-Ni metal in nearly equal proportions. However, since discovery of the closely related acapulcoite group, lodranites Clan

Found 1985, recognized 1990
32° 30.2′ N., 102° 44.6′ W.
While plowing, Mr. Joe D. Nevill unearthed a 524.5 g, moderately weathered stone about 18 miles NW of Andrews, Texas (McCoy et al., 1996). Five years later, in 1990, Dr. Vestal Yeats of Texas Technical University removed a 123.9 g end section and sent it to Glenn Huss for analysis, with the main massLargest fragment of a meteorite, typically at the time of recovery. Meteorites are commonly cut, sliced or sometimes broken thus reducing the size of the main mass and the resulting largest specimen is called the "largest known mass". being retained by Mr. Nevill. The 123.9 g end piece was cut into three sections, and these were distributed among Yeats (H498.2), Huss (H498.1), and Texas Tech (H498.3). The photo below shows this original end piece with lines drawn to show the three-way split. A photo showing the main mass mirror image of the Yeats end section can be seen here, while a different complete slice can be seen here.

 

 

 

 

 

 

 

Dr. Yeats subsequently traded his portion to Walter Zeitschel in Germany. Polished thin sections were made for analyses, three from the Huss specimen and one from the Zeitschel specimen. The photo below shows an excellent petrographic micrograph of the Zeitschel polished thin sectionThin slice or rock, usually 30 µm thick. Thin sections are used to study rocks with a petrographic microscope., shown courtesy of Peter Marmet. In the micrograph the abundant FeNi–FeS–phosphate veins are displayed as dark areas.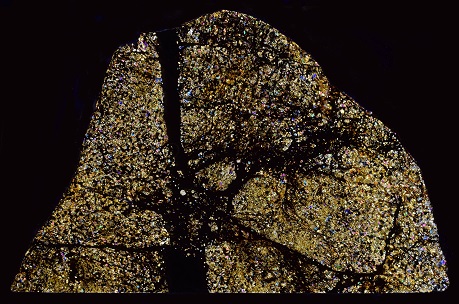

Photo courtesy of Peter Marmet In 2000, the main mass of Monument Draw was sold by Mr. Nevill to International MeteoriteWork in progress. A solid natural object reaching a planet’s surface from interplanetary space. Solid portion of a meteoroid that survives its fall to Earth, or some other body. Meteorites are classified as stony meteorites, iron meteorites, and stony-iron meteorites. These groups are further divided according to their mineralogy and Brokerage, with the vast majority of the material slated for trade to research institutions. The photo at the top of this page shows a 1.55 g thin partial slice acquired from International Meteorite Brokerage, while the photo below shows a slightly more complete section still in the possession of International Meteorite Brokerage. The location on the main mass from which this slice was taken contains a richer portion of the FeNi-metal vein than that which was employed for the thin section shown above.

The parent bodyThe body from which a meteorite or meteoroid was derived prior to its ejection. Some parent bodies were destroyed early in the formation of our Solar System, while others like the asteroid 4-Vesta and Mars are still observable today. of Monument Draw had a unique chondritic composition comprising various chondruleRoughly spherical aggregate of coarse crystals formed from the rapid cooling and solidification of a melt at  ~1400 ° C. Large numbers of chondrules are found in all chondrites except for the CI group of carbonaceous chondrites. Chondrules are typically 0.5-2 mm in diameter and are usually composed of olivine types, high concentrations of planetary-type noble gasesElement occurring in the right-most column of the periodic table; also called "inert" gases. In these gases, the outer electron shell is completely filled, making them very unreactive., and a chondritic mineralogy (A. Rubin, 2007). Many features of acapulcoitesPrimitive achondrite that belongs to a small group named after the Acapulco meteorite that was observed to fall in Mexico in 1976. Acapulcoites are made mostly of fine-grained olivine (Fo3-14), orthopyroxene(En86-97), Ca-rich pyroxene (En51Wo44), plagioclase (An12-31), Ni-Fe metal, and troilite. They are transitional between primordial chondritic matter and more differentiated are similar to CR carbonaceous chondritesChondrites are the most common meteorites accounting for ~84% of falls. Chondrites are comprised mostly of Fe- and Mg-bearing silicate minerals (found in both chondrules and fine grained matrix), reduced Fe/Ni metal (found in various states like large blebs, small grains and/or even chondrule rims), and various refractory inclusions (such, including a high abundance of refractory lithophiles, a high modal abundance of FeNi-metal, chondrule diameters ~700 µm, and, along with lodranites, O-isotopic compositions that overlap the CR field. However, differences do exist between CR chondrites and acapulcoites, including both a higher FeNi-metal and FeS abundance in acapulcoites. Notably, the chondriteChondrites are the most common meteorites accounting for ~84% of falls. Chondrites are comprised mostly of Fe- and Mg-bearing silicate minerals (found in both chondrules and fine grained matrix), reduced Fe/Ni metal (found in various states like large blebs, small grains and/or even chondrule rims), and various refractory inclusions (such Grove Mountains (GRV) 020043, initially classified as H4, is most similar to primitive achondrites based on both its mineralogy and with respect to its O- and Cr-isotopic composition, and may represent the chondritic precursor of the primitive acapulcoite–lodranite clan (Li et al., 2010, abstract; Li et al., 2018).

The differences that do exist between GRV 020043 and ACA–LOD clan, such as in the elements V, Cr, and Se, could be related to specific characteristics of the precursor material (Hidaka et al., 2012). Conversely, based on siderophile elementLiterally, "iron-loving" element that tends to be concentrated in Fe-Ni metal rather than in silicate; these are Fe, Co, Ni, Mo, Re, Au, and PGE. These elements are relatively common in undifferentiated meteorites, and, in differentiated asteroids and planets, are found in the metal-rich cores and, consequently, extremely rare on abundances in magnetic components and lithophile elementElement that tends to be concentrated in the silicate phase, e.g., B, O, halogens, alkali earths, alkali metals, Al, Si, Sc, Ti, V, Cr, Mn, Y, Zr, Nb, REE, Hf, Ta, W, Th, and U. abundances in non-magnetic components, Hidaka et al. (2012) concluded that the precursor material of the acapulcoite–lodranite group was most similar to EL chondrites. Schrader et al. (2017) observed an absence of chromiteBrownish-black oxide of chromium and iron (Cr-Fe oxide), Cr2FeO4, found in many meteorite groups. grains in relict chondrulesRoughly spherical aggregate of coarse crystals formed from the rapid cooling and solidification of a melt at  ~1400 ° C. Large numbers of chondrules are found in all chondrites except for the CI group of carbonaceous chondrites. Chondrules are typically 0.5-2 mm in diameter and are usually composed of olivine from acapulcoite GRA 98028. They recognized that chromite grains are only present in type II chondrules, and that these occur in greatest abundance in ordinary chondrites but are less abundant in carbonaceous and enstatiteA mineral that is composed of Mg-rich pyroxene, MgSiO3. It is the magnesium endmember of the pyroxene silicate mineral series - enstatite (MgSiO3) to ferrosilite (FeSiO3). chondrites. Based on this reasoning as well as other data, they consider it likely that the precursor of acapulcoites was similar to a carbonaceous chondriteCarbonaceous chondrites represent the most primitive rock samples of our solar system. This rare (less than 5% of all meteorite falls) class of meteorites are a time capsule from the earliest days in the formation of our solar system. They are divided into the following compositional groups that, other than of a type unknown in our collections. On the other hand, Keil and McCoy (2017) consider an S-type asteroid to be the most likely parental source object.

Monument Draw has a recrystallized texture with abundant 120° triple junctions, and has an average grain size of ~150–230 µm, the full range of which is similar to that of other acapulcoites (McCoy et al., 1996). In contrast, the genetically related lodranites experienced higher temperatures (up to 1200°C and ~20% partial meltingAn igneous process whereby rocks melt and the resulting magma is comprised of the remaining partially melted rock (sometimes called restite) and a liquid whose composition differs from the original rock. Partial melting occurs because nearly all rocks are made up of different minerals, each of which has a different melting), slower cooling, and greater diffusionMovement of particles from higher chemical potential to lower chemical potential (chemical potential can in most cases of diffusion be represented by a change in concentration). Diffusion, the spontaneous spreading of matter (particles), heat, or momentum, is one type of transport phenomena. Because diffusion is thermally activated, coefficients for diffusion rates leading to more efficient grain growth during contact with a silicateThe most abundant group of minerals in Earth's crust, the structure of silicates are dominated by the silica tetrahedron, SiO44-, with metal ions occurring between tetrahedra). The mesodesmic bonds of the silicon tetrahedron allow extensive polymerization and silicates are classified according to the amount of linking that occurs between the partial melt. Accordingly, they have a larger average grain size of ~540–700 µm. However, with the many new members available for study, it is now evident that a continuum exists for the grain sizes of these two groups, and it has been proposed by Bunch et al. (2011) that an arbitrary group division is no longer justified; the term ‘acapulcoite–lodranite clan’ should therefore be applied to all members of the combined group.

Compared to ordinary chondrites, the ACA–LOD parent body was heated to higher temperatures, reflecting either an earlier accretionAccumulation of smaller objects into progressively larger bodies in the solar nebula leading to the eventual formation of asteroids, planetesimals and planets. The earliest accretion of the smallest particles was due to Van der Waals and electromagnetic forces. Further accretion continued by relatively low-velocity collisions of smaller bodies in the with a proportionately higher abundance of radiogenic elements such as 26Al, or, as elucidated by A. Rubin (2007) and J. T. Wasson (2016), by impact heating. Since some acapulcoites have ages younger than that which is attributed to the complete extinctionIn astronomy, the dimming of starlight as it passes through the interstellar medium. Dust scatters some of the light, causing the total intensity of the light to diminish. It is important to take this effect into account when measuring the apparent brightness of stars. The dark bands running across portions of radiogenic 26Al, the former theory would be less plausible given a scenario involving primarily a radiogenic heat source.

By applying the Hf–W chronometer and integrating its relatively higher closure temperatures, an age of ~6 m.y. after CAISub-millimeter to centimeter-sized amorphous objects found typically in carbonaceous chondrites and ranging in color from white to greyish white and even light pink. CAIs have occasionally been found in ordinary chondrites, such as the L3.00 chondrite, NWA 8276 (Sara Russell, 2016). CAIs are also known as refractory inclusions since they formation is derived for acapulcoite differentiationA process by which a generally homogeneous chondritic body containing mostly metal, silicates and sulfides will melt and form distinct (differentiated) layers of different densities.   When the melting process continues for a long enough period of time, the once chondritic body will re-partition into layers of different composition including, corresponding to an absolute age of 4.5635 (±0.0007) b.y. A slightly older Hf–W age of 3.84 (+3.6/–3.1) m.y. after CAI formation was calculated by Schulz et al. (2010). With other factors considered, they concluded that the metalElement that readily forms cations and has metallic bonds; sometimes said to be similar to a cation in a cloud of electrons. The metals are one of the three groups of elements as distinguished by their ionization and bonding properties, along with the metalloids and nonmetals. A diagonal line drawn melting pointTemperature at which a solid changes to a liquid. A completely pure crystalline substance has an exact temperature at which it melts. Impure substances and amorphous substances will begin melting at one temperature and finish at another. For these substances the term "melting range" is more appropriate. Under some conditions, or the cooling point at which redistribution of Hf and W between metal and silicate ended, occurred 4.1 (+1.2/–1.1) m.y. after CAIsSub-millimeter to centimeter-sized amorphous objects found typically in carbonaceous chondrites and ranging in color from white to greyish white and even light pink. CAIs have occasionally been found in ordinary chondrites, such as the L3.00 chondrite, NWA 8276 (Sara Russell, 2016). CAIs are also known as refractory inclusions since they.

When coupled with Pb–Pb isochron data, it is evident that cooling rates were similar to those of H4 chondrites (Kleine et al., 2007); cooling rates of 65°C/m.y. and 100°C/m.y. were determined by Touboul et al. (2008) and Schulz et al. (2008), respectively. Using multiple chronometers and the Kelvin systemDefinable part of the universe that can be open, closed, or isolated. An open system exchanges both matter and energy with its surroundings. A closed system can only exchange energy with its surroundings; it has walls through which heat can pass. An isolated system cannot exchange energy or matter with, Schulz et al. (2010) determined a cooling rate of ~40K/m.y. as temperatures cooled down to ~720K, and then declined at a rate of ~3K/m.y. below that. Considering the similarity of these cooling rates to those of H4–H5 chondrites (although comparatively higher than cooling rates of interior H6 material) and the significantly higher degree of thermal metamorphism experienced by acapulcoites compared to H4 chondrites, an earlier accretion period (1.5–2 m.y. after CAIs) might be demonstrated for the acapulcoites. Furthermore, a smaller acapulcoite parent body size (~40–80 km in diameter) with rapid cooling near the surface could be reasonably inferred. The young ages of other acapulcoites might reflect resetting of these radiometric chronometers through impact shock heating.

In a similar manner, the I–Xe system was employed by Crowther et al. (2009) to calculate the closure age of a sampling of lodranites and an acapulcoite. Having formed deeper and in hotter conditions, lodranites are considered to have cooled slower and experienced phosphate closure later than acapucoites. However, the samples revealed an average absolute closure age of ~4.5582 b.y. relative to Shallowater; one lodranite had a younger closure age of 4.5519 b.y. When coupled with Pb–Pb isochron data from phosphates, rapid cooling was calculated at a rate of 100 (±40)K/m.y. from peak temperatures, while slower cooling ensued below ~720K. This scenario is consistent with petrographic data showing that very rapid cooling was initiated at high temperatures as a collisional disruption event occurred on the parent asteroid, affecting the cooling of both acapulcoite and lodranite source regions. In consideration of the I–Xe and Pb–Pb systems, the earliest this disruption could have occurred is 9.4 m.y. after CAI formation.

Another model for the cooling history of the acapulcoites demonstrates its complexity. Initially, acapulcoites experienced moderate cooling sustained from a high temperature of at least 988°C (Fe–FeS melting point), possibly as high as ~1100°C, down to ~500°C. Thereafter, the acapulcoites entered a period of rapid cooling down to ~400°C, as evidenced by the older Pb–Pb age of Acapulco (4.557 b.y.; Zipfel et al., 1995). Below ~300°C, it began a slow cooling phase as indicated by its younger Ar–Ar age (~4.51 b.y.). Rapid cooling indicates that either the ACA–LOD parent body was smaller than the ordinary chondriteWork in Progress Ordinary chondrites (OCs) are the largest meteorite clan, comprising approximately 87% of the global collection and 78% of all falls (Meteoritical Society database 2018)1. Meteorites & the Early Solar System: page 581 section 6.1 OC of type 5 or 6 with an apparent shock stage of S1, parent bodies, and/or that it experienced a collisional disruption early in its history, forming sub-km- to multi-km-sized fragments, and eventually succumbing to gravitational reassembly. Rubin (2007) suggests that the abundance of planetary-type noble gases is consistent with a rapid cooling phase. The slow cooling period may represent an event which covered the rock with an insulating ejecta blanketGenerally symmetrical apron of ejecta surrounding a crater; it is thick at the crater's rim and thin to discontinuous at the blanket's outer edge..

The mm- to cm-sized metal veins in Monument Draw are almost troilite-free, likely reflecting the segregation of immiscibleThe property of liquids that are mutually insoluble (won't mix together) such as oil and water or metallic and silicate melts. melt phases. They contain associated phosphates, mostly in the form of whitlockite, along with lesser amounts of chlorapatite and minor fluorapatite. An interesting feature of Monument Draw is the preservation of at least one relict chondrule, an ~2 mm radial pyroxeneA class of silicate (SiO3) minerals that form a solid solution between iron and magnesium and can contain up to 50% calcium. Pyroxenes are important rock forming minerals and critical to understanding igneous processes. For more detailed information, please read the Pyroxene Group article found in the Meteoritics & Classification category. chondrule (see photo below). Relict chondrules are rare among acapulcoites, and have been observed in only nine of the members (Keil and McCoy, 2018): ALHA77081, A-881902, GRA 98028 (∼6 vol.%), GSS 032, GRV 020043 (∼37 vol.% [classified as H4]), Monument Draw, NWA 4236, NWA 4816, and Y-74063. The presence of relict chondrules is a feature that suggests acapulcoites are actually metachondrites, based on terminology associated with several newly recognized groups of chondrule-free, texturally evolved chondrites with elemental ratios and O-isotopic compositions showing affinities to existing chondrite groups (Irving et al., 2005). Relict chondrules are only found in the primitive subgroup of acapulcoites, consistent with this subgroup experiencing the lowest equilibration temperatures (950°C) of all acapulcoites, while Acapulco, a member of the typical subgroup, experienced the highest (1170°C). Monument Draw also has the least equilibrated REEOften abbreviated as “REE”, these 16 elements include (preceded by their atomic numbers): 21 scandium (Sc), 39 Yttrium (Y) and the 14 elements that comprise the lanthanides excluding 61 Promethium, an extremely rare and radioactive element. These elements show closely related geochemical behaviors associated with their filled 4f atomic orbital. distribution within the studied group, and it has a 21Ne-based CRE age (~6.8–7.3 m.y.) which is typical of most other acapulcoites and lodranites. Monument Draw Relict Chondrule

Diagram credit: K. Keil and T. McCoy, Chemie der Erde–GeochemistryStudy of the chemical composition of Earth and other planets, chemical processes and reactions that govern the composition of rocks and soils, and the cycles of matter and energy that transport Earth's chemical components in time and space., vol. 78, no. 2, p. 159 (May 2018)
‘Acapulcoite-lodranite meteorites: UltramaficTerm used for silicate minerals with cations predominantly Mg and/or Fe. Mafic minerals are dominated by plagioclase and pyroxene, and also contain smaller amounts of olivine. asteroidal partial melt residues’
(https://doi.org/10.1016/j.chemer.2017.04.004) Metal veins, like those present in Monument Draw, have been intensively studied (e.g., McCoy et al., 1996, 1997, 2006) to gain insight into the early stages of metal segregation and formation of a coreIn the context of planetary formation, the core is the central region of a large differentiated asteroid, planet or moon and made up of denser materials than the surrounding mantle and crust. For example, the cores of the Earth, the terrestrial planets and differentiated asteroids are rich in metallic iron-nickel. on an asteroid. With a lack of shock indicators and brecciationThe formation of a breccia through a process by which rock fragments of of various types are recemented or fused together. in acapulcoites, and evidence for a significant degree of heating on its parent body, it has commonly been considered that it was heated noncollisionally by either short-lived radiogenic nuclides (e.g., 26Al, 60Fe), or by electrical conductionTransfer of heat as a result of collisions between molecules; when one end of an object is heated or excited, the molecules vibrate faster and their energy is transferred sequentially to their neighbors. by the T-Tauri solar windSupersonic flow of high-speed charged particles continuously blowing off a star (mostly e- and p+). When originating from stars other than the Sun, it is sometimes called a "stellar" wind. The solar wind may be viewed as an extension of the corona into interplanetary space. The solar wind emanates radially. Monument Draw is unshocked (S1), and most other acapulcoites have shock stages of S1 to S2, or rarely higher; these shock effects are attributed to post-annealing shock (Rubin, 2007).

In light of these disparate results, an in-depth review of a shock-melting model for acapulcoites and lodranites was conducted by Rubin (2007). He has clearly demonstrated that impact-heating played a significant role in the petrogenesis of the acapulcoites, and that post-shock annealing has erased all evidence of the shock indicators. For example, Rubin (2006, 2007) has propounded an impact heating theory to explain the diverse content of opaque phases and relict chondrules found among different acapulcoites, and he attributes these features to impact-shock heating followed by rapid cooling. He also ascribes a shock melt origin to the presence of the FeNi–FeS veins, as well as other relict shock features including the following:

1. curvilinear trails of troiliteBrass colored non-magnetic mineral of iron sulfide, FeS, found in a variety of meteorites. blebs within silicate grains
2. metal–sulfide veins
3. polycrystalline metallic phases
4. rapidly crystallized metal–troilite assemblages
5. metallic Cu precipitates
6. Cr veinlets within silicates
7. Cr-plagioclase assemblages

The rapid cooling that ensued is consistent with both an impact scenario and a parent body breakup scenario, while post-shock annealing below an insulating ejectaFractured and/or molten rocky debris thrown out of a crater during a meteorite impact event, or, alternatively, material, including ash, lapilli, and bombs, erupted from a volcano. blanket could account for the appearance of uncorrupted olivineGroup of silicate minerals, (Mg,Fe)2SiO4, with the compositional endpoints of forsterite (Mg2SiO4) and fayalite (Fe2SiO4). Olivine is commonly found in all chondrites within both the matrix and chondrules, achondrites including most primitive achondrites and some evolved achondrites, in pallasites as large yellow-green crystals (brown when terrestrialized), in the silicate portion crystal lattices.

The Monument Draw acapulcoite experienced a low degree of partial melting, ~2–3 vol%, and only a few other meteorites exhibit this same low degree of partial melting and melt migration. One such meteorite is the acapulcoite LEW 86220, which contains a component of trapped FeNi–FeS+plagioclase–pyroxene partial melt. It is inferred that this metallic+basaltic partial melt phase migrated from a great distance given the fact that its lodranite source rock would likely have been a few hundred degrees hotter than the LEW 86220 acapulcoite host rock (McCoy et al., 1997). Notably, the silicate-rich melt having the highest temperature, FRO 93001, was formed through a high-degree partial melt (at least 35 wt%). It contains coarser grains with abundant enstatite, and preserves lodranitic xenoliths (Folco et al., 2006).

Another meteorite that preserves the stage of low degree partial melting and melt migration is the lodranite GRA 95209. While this meteorite is classified as a lodranite based on petrography, it has a bulk composition more consistent with the characteristics of acapulcoites (high metal content of silicates, high Zn content of chromite, etc.), and so was designated a transitional member of the clan along with two other similar meteorites EET 84302 and ALHA81187 (Chikami, 2001). By utilizing X-ray computed tomography techniques, W. Carlson (University of Texas at Austin) constructed a 3-D map of a 554 g mass of GRA 95209 presented as a rotational movie). It shows that the mass comprises three separate lithologies; 1) a predominant metal–silicate matrixFine grained primary and silicate-rich material in chondrites that surrounds chondrules, refractory inclusions (like CAIs), breccia clasts and other constituents., 2) metal-poor zones, and 3) metallic veins. A particularly large metallic sheet, the supposed product of a low-degree partial melt, is considered to have intruded the matrix region from an outlying melt source, perhaps migrating from as far away as hundreds of meters. Poorly graphitized carbonElement commonly found in meteorites, it occurs in several structural forms (polymorphs). All polymorphs are shown to the left with * indicating that it been found in meteorites and impact structures: a. diamond*; b. graphite*; c. lonsdalite*; d. buckminsterfullerene* (C60); e. C540; f. C70; g. amorphous carbon; h. carbon nanotube*. rosettes, measuring up to ~3 mm in diameter, have been identified within the metallic veins and sheet, along with phosphates such as chladniite and various mineralInorganic substance that is (1) naturally occurring (but does not have a biologic or man-made origin) and formed by physical (not biological) forces with a (2) defined chemical composition of limited variation, has a (3) distinctive set of of physical properties including being a solid, and has a (4) homogeneous phases constituting Fe–Mg–Mn-phosphates (McCoy et al., 2006).

This same study of GRA 95209 by McCoy et al. (2006) revealed that an extreme heterogeneity exists in the 13C composition of poorly graphitized carbon in the metal-poor lithology, even within a single metal grain. The investigators speculated that this carbon may have been formed in one of two ways: 1) by parent body processes involving an initial formation of carbonates involving aqueous alteration processes, their subsequent thermal decomposition, the production of elemental carbon via the Fischer–Tropsch-type process (i.e., outgassing CO dissociates at the surface of a metal grain to form a range of carbon-bearing products), and finally, the absorptionTransfer of energy to a medium as a particle or electromagnetic radiation passes through it. Absorption of electromagnetic radiation is the combined result of Compton scattering, σ, and photoelectric absorption, τ. It may be quantified: where, t = thickness, ρ = density, and μ = mass absorption coefficient, which combines Compton and photoelectric effects (μ = σ + τ). of poorly graphitized carbon into molten metal grains; or 2) formation of carbon by the Fischer–Tropsch-type process in the nebulaAn immense interstellar, diffuse cloud of gas and dust from which a central star and surrounding planets and planetesimals condense and accrete. The properties of nebulae vary enormously and depend on their composition as well as the environment in which they are situated. Emission nebula are powered by young, massive, isotopic fractionationConcentration or separation of one mineral, element, or isotope from an initially homogeneous system. Fractionation can occur as a mass-dependent or mass-independent process. and enrichment of 13C (or alternatively, utilizing 13C-rich precursor material), culminating in accretion to the ACA–LOD parent body, before or after its incorporation into a metallic melt phase. In contrast to the isotopically heterogeneous carbon within the metal-poor lithology, the 13C isotopic values of poorly graphitized carbon in the metallic sheet indicate that a high degree of thermal equilibration occurred at a minimum temperature of ~1150°C. This poorly graphitized carbon is consistent with an origin on the parent body.

In his study, Rubin (2007) found that carbon from primary graphiteOpaque form of carbon (C) found in some iron and ordinary chondrites and in ureilite meteorites. Each C atom is bonded to three others in a plane composed of fused hexagonal rings, just like those in aromatic hydrocarbons. The two known forms of graphite, α (hexagonal) and β (rhombohedral), have was probably responsible for an inconstant degree of reductionOxidation and reduction together are called redox (reduction and oxidation) and generally characterized by the transfer of electrons between chemical species, like molecules, atoms or ions, where one species undergoes oxidation, a loss of electrons,  while another species undergoes reduction, a gain of electrons. This transfer of electrons between reactants among the acapulcoites and lodranites, which occurred at high temperatures. Among the indications that reduction occurred are increased metal/troilite ratios, decreased Fa/Fs ratios, decreased FeO/MnO ratios, reversed zoning of some silicate grains (Monument Draw exhibits no reversed zoning), and increased orthopyroxeneOrthorhombic, low-Ca pyroxene common in chondrites. Its compositional range runs from all Mg-rich enstatite, MgSiO3 to Fe-rich ferrosilite, FeSiO3. These end-members form an almost complete solid solution where Mg2+ substitutes for Fe2+ up to about 90 mol. % and Ca substitutes no more than ~5 mol. % (higher Ca2+ contents occur/olivine ratios.

Basaltic partial melt material complimentary to the residual lodranite rock has not been identified so far, probably owing to the fact that it was removed from the ACA–LOD parent body during the early period of its history. This scenario would be consistent with either explosive volcanism, given a small (~70–200 km in diameter; Touboul et al., 2009), volatile-rich asteroid, or impact-induced erosionRemoval of weathered rocks by moving water, wind, or ice. of basaltic surface deposits.

Irving et al. (2005) have described this meteorite as a metamorphosed chondrite probably representing the regolithMixture of unconsolidated rocky fragments, soil, dust and other fine granular particles blanketing the surface of a body lacking an atmosphere. Regolith is the product of "gardening" by repeated meteorite impacts, and thermal processes (such as repeated heating and cooling cycles).   of the acapulcoite–lodranite parent body. Furthermore, they argued that the occurrence of distinct chondrules in some members precludes the use of the term achondriteAn achondrite is a type of stony meteorite whose precursor was of chondritic origin and experienced metamorphic and igneous processes. They have a planetary or differentiated asteroidal origin where the chondritic parent body reached a sufficient size that through heating due to radioactive decay of 26Al (aluminum isotope) and gravitational to describe this group, and they suggest that either of the terms—metachondrite or ‘A chondrite’—would be more appropriate to describe these texturally evolved, relict chondrule-bearing meteorites. For more information on formation scenarios for the acapulcoite-lodranite parent body, please visit the Lodran page.