Viral Theorem
Theorem that relates the total kinetic energy of a self-gravitating body due to the motions of its constituent parts (T) to the gravitational potential energyEnergy inherent in the potential for gravitational collapse. The gravitational potential energy of a gas of atoms and molecules is: where R = radius of the ball of gas, and M = total mass. (U) of the body.
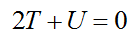
By re-arranging and making some simple assumptions about T and U for galaxies, this becomes:
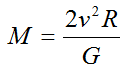
where M is the total mass of the galaxyConcentration of 10 to 10 stars, dust and gas, that are gravitationally bound. Our galaxy contains ~2 × 10 stars. There are four main types of galaxies: • Elliptical
• Lenticular
• Spiral
• Irregular
, v is the mean velocity (combining the rotation and velocity dispersion) of stars in the galaxy, G is Newton’s gravitational constant, and R is the effective radius (size) of the galaxy. This equation relates two observable properties of galaxies (velocity dispersion and effective radius) to a fundamental, but unobservable, property – the mass of the galaxy. The comparison of mass estimates based on the virial theorem to estimates based on the luminosities provides one method of estimating the amount of dark matterForm of matter that does not emit light, absorb light, or otherwise interact with electromagnetic radiation. Its only interactions are gravitational and dark matter particles can clump under the force of gravity (unlike "dark energy" which is evenly distributed throughout space). The existence of dark matter has been inferred from in a galaxy or clusters of galaxies.
